Los prismas son un ejemplo de como la luz se comporta como una onda y por lo tanto sufre los fenómenos ondulatorios, en este caso la refracción, manifiesta en la descomposición de la luz blanca.
La luz es una radiación que se propaga en forma de ondas. Las ondas que se pueden propagar en el vacío se llaman ONDAS ELECTROMAGNÉTICAS. La luz es una radiación electromagnética.

descomposición de colores después de pasar por un prisma triangular.
CARACTERÍSTICAS DE LAS ONDAS ELECTROMAGNÉTICAS
Las ondas electromagnéticas se propagan en el vacío a la velocidad de 300000 km/s, que se conoce como "velocidad de la luz en el vacío" y se simboliza con la letra c (c = 300000 km/s).
La velocidad de la luz en el vacío no puede ser superada por la de ningún otro movimiento existente en la naturaleza. En cualquier otro medio, la velocidad de la luz es inferior.
La energía transportada por las ondas es proporcional a su frecuencia, de modo que cuanto mayor es la frecuencia de la onda, mayor es su energía.
Las ondas electromagnéticas se clasifican según su frecuencia como puede verse en el siguiente diagrama:
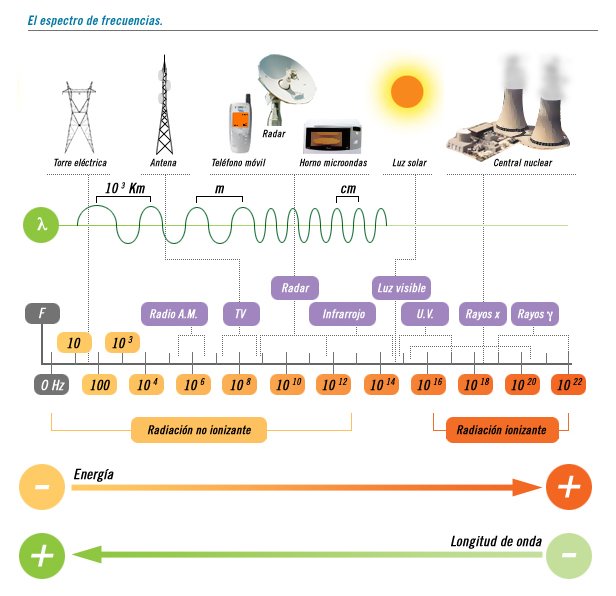
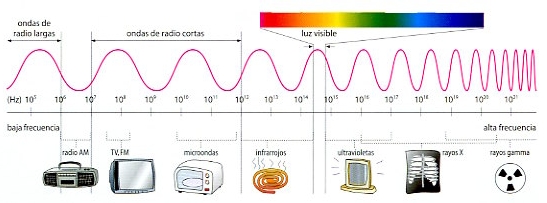
El espectro electromagnético está constituido por todos los posibles niveles de energía que la luz puede tomar. Hablar de energía es equivalente a hablar de longitud de onda; luego, el espectro electromagnético abarca, también, todas las longitudes de onda que la luz pueda tener, desde miles de kilómetros hasta femtómetros. Es por eso que la mayor parte de las representaciones esquemáticas del espectro suelen tener escala logarítmica.
El espectro electromagnético se divide en regiones espectrales, clasificadas según los métodos necesarios para generar y detectar los diversos tipos de radiación. Es por eso que estas regiones no tienen una frontera definida y existen algunos solapamientos entre ellas.
la LUZ es la radiación es la radiación visible del espectro que podemos captar con nuestros ojos.
NATURALEZA DE LA LUZ
La luz presenta una naturaleza compleja: depende de cómo la observemos se manifestará como una onda o como una partícula. Estos dos estados no se excluyen, sino que son complementarios. Sin embargo, para obtener un estudio claro y conciso de su naturaleza, podemos clasificar los distintos fenómenos en los que participa según su interpretación teórica:
TEORÍA ONDULATORIA
DESCRIPCIÓN
Esta teoría, desarrollada por Christiaan Huygens, considera que la luz es una onda electromagnética, consistente en un campo eléctrico que varía en el tiempo generando a su vez un campo magnético y viceversa, ya que los campos eléctricos variables generan campos magnéticos (ley de Ampère) y los campos magnéticos variables generan campos eléctricos (ley de Faraday). De esta forma, la onda se autopropaga indefinidamente a través del espacio, con campos magnéticos y eléctricos generándose continuamente. Estas ondas electromagnéticas son sinusoidales, con los campos eléctrico y magnético perpendiculares entre sí y respecto a la dirección de propagación.


"Vista lateral (izquierda) de una onda electromagnética a lo largo de un instante y vista frontal (derecha) de la misma en un momento determinado. De color rojo se representa el campo magnético y de azul el eléctrico."
Para poder describir una onda electromagnética podemos utilizar los parámetros habituales de cualquier onda:
♦ Amplitud (A): Es la longitud máxima respecto a la posición de equilibrio que alcanza la onda en su desplazamiento.
♦ Periodo (T): Es el tiempo necesario para el paso de dos máximos o mínimos sucesivos por un punto fijo en el espacio.
♦ Frecuencia (ν): Número de oscilaciones del campo por unidad de tiempo. Es una cantidad inversa al periodo.
♦ Longitud de onda (λ): Es la distancia lineal entre dos puntos equivalentes de ondas sucesivas.
♦ Velocidad de propagación (V): Es la distancia que recorre la onda en una unidad de tiempo. En el caso de la velocidad de propagación de la luz en el vacío, se representa con la letra c.
La velocidad, la frecuencia, el periodo y la longitud de onda están relacionadas por las siguientes ecuaciones:
FENÓMENOS ONDULATORIOS
(movimientos ondulatorios)
Algunos de los fenómenos más importantes de la luz se pueden comprender fácilmente si se considera que tiene un comportamiento ondulatorio.
El principio de superposición de ondas nos permite explicar el fenómeno de la interferencia: si juntamos en el mismo lugar dos ondas con la misma longitud de onda y amplitud, si están en fase (las crestas de las ondas coinciden) formarán una interferencia constructiva y la intensidad de la onda resultante será máxima e igual a dos veces la amplitud de las ondas que la conforman. Si están desfasadas, habrá un punto donde el desfase sea máximo (la cresta de la onda coincida exactamente con un valle) formándose una interferencia destructiva, anulándose la onda. El experimento de Young, con sus rendijas, nos permite obtener dos focos de luz de la misma longitud de onda y amplitud, creando un patrón de interferencias sobre una pantalla.
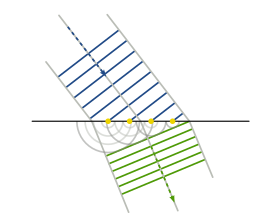
Las ondas cambian su dirección de propagación al cruzar un obstáculo puntiagudo o al pasar por una abertura estrecha. Como recoge el principio de Fresnel - Huygens, cada punto de un frente de ondas es un emisor de un nuevo frente de ondas que se propagan en todas las direcciones. La suma de todos los nuevos frentes de ondas hace que la perturbación se siga propagando en la dirección original. Sin embargo, si por medio de una rendija o de un obstáculo puntiagudo, se separa uno o unos pocos de los nuevos emisores de ondas, predominará la nueva dirección de propagación frente a la original.

La difracción de la luz se explica fácilmente si se tiene en cuenta este efecto exclusivo de las ondas. La refracción, también se puede explicar utilizando este principio, teniendo en cuenta que los nuevos frentes de onda generados en el nuevo medio, no se transmitirán con la misma velocidad que en el anterior medio, generando una distorsión en la dirección de propagación:
Otro fenómeno de la luz fácilmente identificable con su naturaleza ondulatoria es la polarización. La luz no polarizada está compuesta por ondas que vibran en todos los ángulos, al llegar a un medio polarizador, sólo las ondas que vibran en un ángulo determinado consiguen atravesar el medio, al poner otro polarizador a continuación, si el ángulo que deja pasar el medio coincide con el ángulo de vibración de la onda, la luz pasará íntegra, si no sólo una parte pasará hasta llegar a un ángulo de 90º entre los dos polarizadores, donde no pasará nada de luz.

Este efecto, además, permite demostrar el carácter transversal de la luz (sus ondas vibran en dirección perpendicular a la dirección de propagación).
El efecto Faraday y el cálculo de la velocidad de la luz, c, a partir de constantes eléctricas (permitividad, ) y magnéticas (permeabilidad, μ0) por parte de la teoría de Maxwell:
Confirman que las ondas de las que está compuesta la luz son de naturaleza electromagnética. Esta teoría fue capaz, también, de eliminar la principal objeción a la teoría ondulatoria de la luz, que era encontrar la manera de que las ondas se trasladasen sin un medio material.
DESCRIPCIÓN
La teoría corpuscular estudia la luz como si se tratase de un torrente de partículas sin carga y sin masa llamadas fotones, capaces de portar todas las formas de radiación electromagnética. Esta interpretación resurgió debido a que, la luz, en sus interacciones con la materia, intercambia energía sólo en cantidades discretas (múltiples de un valor mínimo) de energía denominadas cuantos. Este hecho es difícil de combinar con la idea de que la energía de la luz se emita en forma de ondas, pero es fácilmente visualizado en términos de corpúsculos de luz o fotones.
FENÓMENOS CORPUSCULARES
Existen tres efectos que demuestran el carácter corpuscular de la luz. Según el orden histórico, el primer efecto que no se pudo explicar por la concepción ondulatoria de la luz fue la radiación del cuerpo negro.
Un cuerpo negro es un radiador teóricamente perfecto que absorbe toda la luz que incide en él y por eso, cuando se calienta se convierte en un emisor ideal de radiación térmica, que permite estudiar con claridad el proceso de intercambio de energía entre radiación y materia. La distribución de frecuencias observadas de la radiación emitida por la caja a una temperatura de la cavidad dada, no se correspondía con las predicciones teóricas de la física clásica. Para poder explicarlo, Max Planck, al comienzo del siglo XX, postuló que para ser descrita correctamente, se tenía que asumir que la luz de frecuencia ν es absorbida por múltiplos enteros de un cuanto de energía igual a hν, donde h es una constante física universal llamada Constante de Planck.
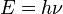
En 1905, Albert Einstein utilizó la teoría cuántica recién desarrollada por Planck para explicar otro fenómeno no comprendido por la física clásica: el efecto fotoeléctrico. Este efecto consiste en que cuando un rayo monocromático de radiación electromagnética ilumina la superficie de un sólido (y, a veces, la de un líquido), se desprenden electrones en un fenómeno conocido como fotoemisión o efecto fotoeléctrico externo. Estos electrones poseen una energía cinética que puede ser medida electrónicamente con un colector con carga negativa conectado a la superficie emisora. No se podía entender que la emisión de los llamados "fotoelectrones" fuese inmediata e independiente de la intensidad del rayo. Eran incluso capaces de salir despedidos con intensidades extremadamente bajas, lo que excluía la posibilidad de que la superficie acumulase de alguna forma la energía suficiente para disparar los electrones. Además, el número de electrones era proporcional a la intensidad del rayo incidente. Einstein demostró que el efecto fotoeléctrico podía ser explicado asumiendo que la luz incidente estaba formada de fotones de energía hν, parte de esta energía hν0 se utilizaba para romper las fuerzas que unían el electrón con la materia, el resto de la energía aparecía como la energía cinética de los electrones emitidos:

Donde m es la masa del electrón, vmáx la velocidad máxima observada, ν es la frecuencia de la luz iluminante y ν0 es la frecuencia umbral característica del sólido emisor.
La demostración final fue aportada por Arthur Compton que observó como al hacer incidir rayos X sobre elementos ligeros, estos se dispersaban con menor energía y además se desprendían electrones (fenómeno posteriormente denominado en su honor como efecto Compton). Compton, ayudándose de las teorías anteriores, le dio una explicación satisfactoria al problema tratando la luz como partículas que chocan elásticamente con los electrones como dos bolas de billar. El fotón, corpúsculo de luz, golpea al electrón: el electrón sale disparado con una parte de la energía del fotón y el fotón refleja su menor energía en su frecuencia. Las direcciones relativas en las que salen despedidos ambos están de acuerdo con los cálculos que utilizan la conservación de la energía y el momento.
Otro fenómeno que demuestra la teoría corpuscular es la presión luminosa.
TEORÍAS CUÁNTICAS
La necesidad de reconciliar las ecuaciones de Maxwell del campo electromagnético, que describen el carácter ondulatorio electromagnético de la luz, con la naturaleza corpuscular de los fotones, ha hecho que aparezcan varías teorías que están aún lejos de dar un tratamiento unificado satisfactorio. Estas teorías incorporan por un lado, la teoría de la electrodinámica cuántica, desarrollada a partir de los artículos de Dirac, Jordán, Heisenberg y Pauli, y por otro lado la mecánica cuántica de Broglie, Heisenberg y Schrödinger.
Paúl Dirac dio el primer paso con su ecuación de ondas que aportó una síntesis de las teorías ondulatoria y corpuscular, ya que siendo una ecuación de ondas electromagnéticas su solución requería ondas cuantizadas, es decir, partículas. Su ecuación consistía en reescribir las ecuaciones de Maxwell de tal forma que se pareciesen a las ecuaciones hamiltonianas de la mecánica clásica. A continuación, utilizando el mismo formalismo que, a través de la introducción del cuanto de acción hν, transforma las ecuaciones de mecánica clásica en ecuaciones de mecánica ondulatoria, Dirac obtuvo una nueva ecuación del campo electromagnético. Las soluciones a esta ecuación requerían ondas cuantizadas, sujetas al principio de incertidumbre de Heisenberg, cuya superposición representaban el campo electromagnético. Gracias a esta ecuación podemos conocer una descripción de la probabilidad de que ocurra una interacción u observación dada, en una región determinada.
Existen aún muchas dificultades teóricas sin resolverse, sin embargo, la incorporación de nuevas teorías procedentes de la experimentación con partículas elementales, así como de teorías sobre el comportamiento de los núcleos atómicos, nos han permitido obtener una formulación adicional de gran ayuda.
el físico estadounidense RICHARD FEYNMAN creo unos de los
diagramas que describen diferentes procesos entre partículas conocidos como diagramas de FEYNMAN; en el caso de la interacción electromagnetica entre nuestro par de electrones, el intercambio de un fotón se representa por el diagrama de la figura.
el fotón es una partícula sin carga eléctrica y sin masa, por lo que se mueve a la velocidad de la luz.
Todas las partículas fundamentalmente tienen ademas una propiedad intriseca (como su masa y su carga eléctrica) llamada ESPÍN. esta propiedad puede visualizarse como el giro de la partícula sobre su eje, así como la tierra gira sobre su eje cada día. sin embargo es importante destacar que esta visualizando en solo una analogía, ya que las partículas elementales son puntuales, no pequeñas esferas que rotan.
el espín es una parte importante que nos ayudara a clasificar a las partículas, y que pueden tomar valores enteros (0,1,2,3,4,5, etc.) o semienteros ( 1/2, 3/2 etc.)
EFECTOS RELATIVISTICOS
Sin embargo, existían aún algunas situaciones en las que la luz no se comportaba según lo esperado por las teorías anteriores.
LUZ EN MOVIMIENTO
La primera de estas situaciones inexplicables se producía cuando la luz se emitía, se transmitía o se recibía por cuerpos o medios en movimiento. Era de esperar, según la física clásica, que la velocidad en estos casos fuese el resultado de sumar a la velocidad de la luz, la velocidad del cuerpo o del medio. Sin embargo, se encontraron varios casos en los que no era así:
En 1818, Augustin Fresnel propuso un experimento para medir la velocidad a la que la luz atravesaba un líquido en movimiento. Para ello, se haría atravesar a la luz una columna de un líquido que fluyese a una velocidad v relativa al observador. Conociendo la velocidad v' a la que se trasmite la luz a través de ese medio (a través del índice de refracción), se calculó que la velocidad total de la luz en ese fluido sería:
es decir, que la velocidad del fluido contaba menos en la velocidad final si la velocidad con la que atravesaba la luz ese fluido era mayor.
DISTORSIONES ESPECTRALES
Al comparar el espectro de la luz procedente de algunos cuerpos celestes, con los espectros medidos en el laboratorio de los mismos elementos que los que contienen esos cuerpos, se observa que no son iguales, ya que las líneas espectrales procedentes del espacio están desplazadas hacia posiciones de mayor longitud de onda, es decir, hacia el lado rojo del espectro en lugares de menor energía.
Se han encontrado dos tipos diferentes de desplazamientos de líneas espectrales:
Uno, el más común, llamado desplazamiento nebular es un desplazamiento sistemático de los espectros procedentes de las estrellas y galaxias. Edwin Hubble tras estudiar el corrimiento de los espectros de las nebulosas, lo interpretó como el resultado del efecto Doppler debido a la expansión continua del universo. Gracias a esto propuso una fórmula capaz de calcular la distancia que nos separa de un cuerpo determinado analizando el corrimiento de su espectro:


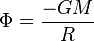







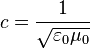




FIGURA 2

LUZ EN MOVIMIENTO
La primera de estas situaciones inexplicables se producía cuando la luz se emitía, se transmitía o se recibía por cuerpos o medios en movimiento. Era de esperar, según la física clásica, que la velocidad en estos casos fuese el resultado de sumar a la velocidad de la luz, la velocidad del cuerpo o del medio. Sin embargo, se encontraron varios casos en los que no era así:
En 1818, Augustin Fresnel propuso un experimento para medir la velocidad a la que la luz atravesaba un líquido en movimiento. Para ello, se haría atravesar a la luz una columna de un líquido que fluyese a una velocidad v relativa al observador. Conociendo la velocidad v' a la que se trasmite la luz a través de ese medio (a través del índice de refracción), se calculó que la velocidad total de la luz en ese fluido sería:
es decir, que la velocidad del fluido contaba menos en la velocidad final si la velocidad con la que atravesaba la luz ese fluido era mayor.
DISTORSIONES ESPECTRALES
Al comparar el espectro de la luz procedente de algunos cuerpos celestes, con los espectros medidos en el laboratorio de los mismos elementos que los que contienen esos cuerpos, se observa que no son iguales, ya que las líneas espectrales procedentes del espacio están desplazadas hacia posiciones de mayor longitud de onda, es decir, hacia el lado rojo del espectro en lugares de menor energía.
Se han encontrado dos tipos diferentes de desplazamientos de líneas espectrales:
Uno, el más común, llamado desplazamiento nebular es un desplazamiento sistemático de los espectros procedentes de las estrellas y galaxias. Edwin Hubble tras estudiar el corrimiento de los espectros de las nebulosas, lo interpretó como el resultado del efecto Doppler debido a la expansión continua del universo. Gracias a esto propuso una fórmula capaz de calcular la distancia que nos separa de un cuerpo determinado analizando el corrimiento de su espectro:

donde Δλ es la diferencia entre las longitudes de onda del espectro del cuerpo y la esperada, λ es la longitud de onda esperada y d, la distancia en pársecs.

Desplazamiento Nebular.
El otro, mucho más extraño se llama desplazamiento gravitacional o efecto Einstein, observado en espectros de cuerpos extremadamente densos.
El ejemplo más famoso es el espectro del llamado compañero oscuro de Sirio. La existencia de este compañero fue predicha por Friedrich Bessel en 1844 basándose en una perturbación que observó en el movimiento de Sirio, pero debido a su débil luminosidad, no fue descubierto hasta 1861. Este compañero es una enana blanca que tiene una masa comparable a la del Sol pero en un radio aproximadamente cien veces menor, por lo que su densidad es inmensa (61.000 veces la del agua). Al estudiarse su espectro, se observa un desplazamiento de 0,3 Å de la línea ß de la serie Balmer del hidrógeno.
El ejemplo más famoso es el espectro del llamado compañero oscuro de Sirio. La existencia de este compañero fue predicha por Friedrich Bessel en 1844 basándose en una perturbación que observó en el movimiento de Sirio, pero debido a su débil luminosidad, no fue descubierto hasta 1861. Este compañero es una enana blanca que tiene una masa comparable a la del Sol pero en un radio aproximadamente cien veces menor, por lo que su densidad es inmensa (61.000 veces la del agua). Al estudiarse su espectro, se observa un desplazamiento de 0,3 Å de la línea ß de la serie Balmer del hidrógeno.
TEORÍA DE LA RELATIVIDAD GENERAL
Para que su anterior teoría de la relatividad especial abarcase también los fenómenos gravitatorios, Albert Einstein, entre 1907 y 1915 desarrolló la teoría de la relatividad general. Una de las principales conclusiones de esta teoría es que la propagación de la luz está influenciada por la gravedad, representada en la teoría por el potencial gravitatorio Φ, descrito por
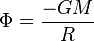
donde G es la Constante de gravitación universal, M la masa y R el radio del cuerpo.
Einstein encontró que la luz, al pasar por un campo gravitatorio de potencial Φ sufría una disminución de su velocidad, según la fórmula:

donde c0 es la velocidad de la luz sin campo gravitatorio y c es la velocidad con él.
También se ve modificada la frecuencia de la luz emitida por una fuente en un campo gravitatorio.

lo que explica el desplazamiento gravitacional. Otro ejemplo que confirma experimentalmente este punto de la teoría son las líneas espectrales del sol, que están desplazadas hacia el rojo dos millonésimas veces cuando sea comparan con las generadas por los mismos elementos en la Tierra.
Por último, en esta relación entre luz y gravedad, esta teoría predijo que los rayos de luz al pasar cerca de un cuerpo pesado se desviaba un ángulo α determinado por el efecto de su campo gravitatorio, según la relación:

Este punto de la teoría fue confirmado experimentalmente estudiando el desvío de la luz que provocaba el sol, para ello los científicos estudiaron la posición de las estrellas del área alrededor del sol aprovechando un eclipse en 1931. Se vio que, como predecía la teoría, estaban desviadas hasta 2,2 segundos de arco comparadas con fotos de la misma área 6 meses antes.
RADIACIÓN Y MATERIA
Al formular su ecuación de ondas para un electrón libre, Paúl Dirac predijo que era posible crear un par de electrones (uno cargado positivamente y otro negativamente) a partir de un campo electromagnético que vibrase extremadamente rápido. Esta teoría fue rápidamente confirmada por los experimentos de Irene Curie y Frédéric Joliot y por los de James Chadwick, Stuart Blackett y Giuseppe Occhialini al comparar el número de electrones con carga negativa y el número de electrones con carga positiva (estos últimos llamados positrones) desprendidos por los rayos γ de alta frecuencia al atravesar delgadas láminas de plomo y descubrir que se obtenía la misma cantidad de unos que de los otros.
Pronto se encontraron otras formas de crear pares positrón-electrón y hoy en día se conocen una gran cantidad de métodos:
♦Haciendo chocar dos partículas pesadas.
♦Haciendo pasar a un electrón a través del campo de un núcleo atómico.
♦La colisión directa de dos electrones.
♦La colisión directa de dos fotones en el vacío.
♦La acción del campo de un núcleo atómico sobre un rayo γ emitido por el mismo núcleo.
También ocurre el proceso en sentido contrario: al colisionar un electrón y un positrón (ellos solos tienden a juntarse, ya que tienen cargas eléctricas opuestas), ambos se aniquilan convirtiendo toda su masa en energía radiante. Esta radiación se emite en forma de dos fotones de rayos γ dispersados en la misma dirección, pero diferente sentido.
Esta relación entre materia-radiación, y viceversa (y sobre todo la conservación de la energía en esta clase de procesos) está descrita en la famosa ecuación de Albert Einstein:

enmarcada en la teoría de la relatividad especial y que originalmente formuló así:
Si un cuerpo de masa m desprende una cantidad de energía E en forma de radiación, su masa disminuye E / c2.
TEORÍA DE CAMPO UNIFICADO
Actualmente, se busca una teoría que sea capaz de explicar de forma unificada la relación de la luz, como campo electromagnético, con el resto de las interacciones fundamentales de la naturaleza. Las primeras teorías intentaron representar el electromagnetismo y la gravitación como aspectos de la geometría espacio-tiempo, y aunque existen algunas evidencias experimentales de una conexión entre el electromagnetismo y la gravitación, sólo se han aportado teorías especulativas.
VELOCIDAD DE LA LUZ

la luz solar tarda aproximadamente 8 minutos y 19 segundos en llegar a la tierra.
La velocidad de la luz en el vacío es por definición una constante universal de valor 299.792.458 m/s2 3 (suele aproximarse a 3·108 m/s), o lo que es lo mismo 9,46·1015 m/año; la segunda cifra es la usada para definir al intervalo llamado año luz.
Se simboliza con la letra c, proveniente del latín celéritās (en español celeridad o rapidez), y también es conocida como la constante de Einstein.
El valor de la velocidad de la luz en el vacío fue incluida oficialmente en el Sistema Internacional de Unidades como constante el 21 de octubre de 1983, pasando así el metro a ser una unidad derivada de esta constante.
La rapidez a través de un medio que no sea el "vacío" depende de su permitividad eléctrica, de su permeabilidad magnética, y otras características electromagnéticas. En medios materiales, esta velocidad es inferior a "c" y queda codificada en el índice de refracción. En modificaciones del vacío más sutiles, como espacios curvos, efecto Casimir, poblaciones térmicas o presencia de campos externos, la velocidad de la luz depende de la densidad de energía de ese vacío.
DESCRIPCIÓN EN GENERAL
De acuerdo con la física moderna estándar, toda radiación electromagnética (incluida la luz visible) se propaga o mueve a una velocidad constante en el vacío, conocida común como la "velocidad de la luz" (magnitud vectorial), en vez de "rapidez de la luz" (magnitud escalar). Ésta es una constante física denotada como c. La rapidez c es también la rapidez de la propagación de la gravedad en la Teoría general de la relatividad.
Una consecuencia en las leyes del electromagnetismo (tales como las ecuaciones de Maxwell) es que la rapidez c de radiación electromagnética no depende de la velocidad del objeto que emite la radiación. Así, por ejemplo, la luz emitida de una fuente de luz que se mueve rápidamente viajaría a la misma velocidad que la luz proveniente de una fuente estacionaria (aunque el color, la frecuencia, la energía y el momentum de la luz cambiarán; fenómeno que se conoce como efecto Doppler).Si se combina esta observación con el principio de relatividad, se concluye que todos los observadores medirán la velocidad de la luz en el vacío como una misma, sin importar el marco de referencia del observador o la velocidad del objeto que emite la luz. Debido a esto, se puede ver a c como una constante física fundamental. Este hecho, entonces, puede ser usado como base en la teoría de relatividad especial. La constante es la rapidez c, en vez de la luz en sí misma, lo cual es fundamental para la relatividad especial. De este modo, si la luz es de alguna manera retardada para viajar a una velocidad menor a c, esto no afectará directamente a la teoría de relatividad especial.Observadores que viajan a grandes velocidades encontrarán que las distancias y los tiempos se distorsionan de acuerdo con la transformación de Lorentz. Sin embargo, las transformaciones distorsionan tiempos y distancias de manera que la velocidad de la luz permanece constante. Una persona viajando a una velocidad cercana a c también encontrará que los colores de la luz al frente se tornan azules y atrás se tornan rojos.Si la información pudiese viajar más rápido que c en un marco de referencia, la causalidad sería violada: en otros marcos de referencia, la información sería recibida antes de ser mandada; así, la causa podría ser observada después del efecto. Debido a la dilatación del tiempo de la relatividad especial, el cociente del tiempo percibido entre un observador externo y el tiempo percibido por un observador que se mueve cada vez más cerca de la velocidad de la luz se aproxima a cero. Si algo pudiera moverse más rápidamente que luz, este cociente no sería un número real. Tal violación de la causalidad nunca se ha observado.Existe, sin embargo, un experimento inquietante realizado por los científicos del "NEC Research Institute at Princeton ", los cuales afirman haber logrado pulsos de luz a una rapidez 300 veces superior a c.(Es necesario notar que se trata de un experimento no confirmado ni publicado aún).

cono de luz futuro y pasado de un evento cualquiera.
Es una representación cualquiera del espacio-tiempo con arreglo a la teoría de la relatividad especial. según dicha teoría, el cono de luz es un modelo útil para describir la evolución en el tiempo de un haz luminoso en el espacio-tiempo de minkowski. el fenómeno real cuadrimensional (tres dimensiones espaciales mas la dimensión temporal).
el cono de luz sirve asimismo como representación del principio de casualidad, que enlaza entre si causa y efecto de los fenómenos.
DESCRIPCIÓN EN GENERAL
De acuerdo con la física moderna estándar, toda radiación electromagnética (incluida la luz visible) se propaga o mueve a una velocidad constante en el vacío, conocida común como la "velocidad de la luz" (magnitud vectorial), en vez de "rapidez de la luz" (magnitud escalar). Ésta es una constante física denotada como c. La rapidez c es también la rapidez de la propagación de la gravedad en la Teoría general de la relatividad.
Una consecuencia en las leyes del electromagnetismo (tales como las ecuaciones de Maxwell) es que la rapidez c de radiación electromagnética no depende de la velocidad del objeto que emite la radiación. Así, por ejemplo, la luz emitida de una fuente de luz que se mueve rápidamente viajaría a la misma velocidad que la luz proveniente de una fuente estacionaria (aunque el color, la frecuencia, la energía y el momentum de la luz cambiarán; fenómeno que se conoce como efecto Doppler).Si se combina esta observación con el principio de relatividad, se concluye que todos los observadores medirán la velocidad de la luz en el vacío como una misma, sin importar el marco de referencia del observador o la velocidad del objeto que emite la luz. Debido a esto, se puede ver a c como una constante física fundamental. Este hecho, entonces, puede ser usado como base en la teoría de relatividad especial. La constante es la rapidez c, en vez de la luz en sí misma, lo cual es fundamental para la relatividad especial. De este modo, si la luz es de alguna manera retardada para viajar a una velocidad menor a c, esto no afectará directamente a la teoría de relatividad especial.Observadores que viajan a grandes velocidades encontrarán que las distancias y los tiempos se distorsionan de acuerdo con la transformación de Lorentz. Sin embargo, las transformaciones distorsionan tiempos y distancias de manera que la velocidad de la luz permanece constante. Una persona viajando a una velocidad cercana a c también encontrará que los colores de la luz al frente se tornan azules y atrás se tornan rojos.Si la información pudiese viajar más rápido que c en un marco de referencia, la causalidad sería violada: en otros marcos de referencia, la información sería recibida antes de ser mandada; así, la causa podría ser observada después del efecto. Debido a la dilatación del tiempo de la relatividad especial, el cociente del tiempo percibido entre un observador externo y el tiempo percibido por un observador que se mueve cada vez más cerca de la velocidad de la luz se aproxima a cero. Si algo pudiera moverse más rápidamente que luz, este cociente no sería un número real. Tal violación de la causalidad nunca se ha observado.Existe, sin embargo, un experimento inquietante realizado por los científicos del "NEC Research Institute at Princeton ", los cuales afirman haber logrado pulsos de luz a una rapidez 300 veces superior a c.(Es necesario notar que se trata de un experimento no confirmado ni publicado aún).

cono de luz futuro y pasado de un evento cualquiera.
Es una representación cualquiera del espacio-tiempo con arreglo a la teoría de la relatividad especial. según dicha teoría, el cono de luz es un modelo útil para describir la evolución en el tiempo de un haz luminoso en el espacio-tiempo de minkowski. el fenómeno real cuadrimensional (tres dimensiones espaciales mas la dimensión temporal).
el cono de luz sirve asimismo como representación del principio de casualidad, que enlaza entre si causa y efecto de los fenómenos.
el cono de luz se diseña del siguiente modo:
Tomando como evento P un haz luminoso ( o pulso de luz ) en un tiempo 0 ( el punto convergente de los ejes del gráfico ), todos los acontecimientos que dicho pulso es capaz de alcanzar desde el punto P forman el cono de luz futuro de P, mientras que aquellos eventos capaces de enviar un pulso de luz hasta P forman el cono de luz pasado de P. El vértice de dicho cono, a afecto de representación, es de 45 grados.
dado un evento cualquiera E, el cono de luz clasifica todos los eventos espacio-temporales en cinco categorías distintas:
♦ eventos en el cono de luz futuro de E, a los que pueden alcanzar la luz desde E.
♦ eventos en el cono de luz pasado de E, desde los cuales la luz pudo haber llegado a E.
♦ eventos dentro del cono de luz del futuro de E, que están afectados por una partícula emitida "desde" E.
♦ eventos dentro del cono de luz pasado de E que pueden haber emitido una particula material y afectar a lo que ocurre en E.
♦ todos los demás eventos que se encuentran en "cualquier otro sitio", mas allá de los conos de E, y que nunca afectaran ni podrán ser afectados casualmente por lo que suceden en E.
de acuerdo a la definición actual, adoptada en 1938, la rapidez de la luz es exactamente 299.792.458 m/s (aproximadamente 3 × 108 metros por segundo, 300.000 km/s o 300 m por millonésimas de s.)
El valor de c define la permitividad eléctrica del vacío 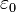 en unidades del SIU como:
en unidades del SIU como:
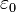 en unidades del SIU como:
en unidades del SIU como:
La permeabilidad magnética del vacío (μ0) no es dependiente de c y es definida en unidades del SIU como:

Estas constantes aparecen en las ecuaciones de Maxwell, que describen el electromagnetismo y están relacionadas por:
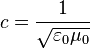
Las distancias astronómicas son normalmente medidas en años luz (que es la distancia que recorre la luz en un año, aproximadamente 9,454256 × 1012 km (9 billones de km).
COMUNICACIONES

La velocidad de la luz es de gran importancia para las telecomunicaciones. Por ejemplo, dado que el perímetro de la Tierra es de 40.075 km (en la línea ecuatorial) y c es teóricamente la velocidad más rápida en la que un fragmento de información puede viajar, el período más corto de tiempo para llegar al otro extremo del globo terráqueo sería 0,067 s.
En la actualidad el tiempo de viaje es un poco más largo, en parte debido a que la velocidad de la luz es cerca de un 30% menor en una fibra óptica, y raramente existen trayectorias rectas en las comunicaciones globales; además se producen retrasos cuando la señal pasa a través de interruptores eléctricos o generadores de señales. En 2004, el retardo típico de recepción de señales desde Australia o Japón hacia los EE.UU. era de 0,18 s. Adicionalmente, la velocidad de la luz afecta al diseño de las comunicaciones inalámbricas.
La velocidad finita de la luz se hizo aparente a todo el mundo en el control de comunicaciones entre el Control Terrestre de Houston y Neil Armstrong, cuando éste se convirtió en el primer hombre que puso un pie sobre la Luna: después de cada pregunta, Houston tenía que esperar cerca de 3 s para el regreso de una respuesta aún cuando los astronautas respondían inmediatamente.
De manera similar, el control remoto instantáneo de una nave interplanetaria es imposible debido a que una nave suficientemente alejada de nuestro planeta podría tardar algunas horas desde que envía información al centro de control terrestre y recibe las instrucciones.
La velocidad de la luz también puede tener influencia en distancias cortas. En los superordenadores la velocidad de la luz impone un límite de rapidez a la que pueden ser enviados los datos entre procesadores. Si un procesador opera a1 GHz, la señal sólo puede viajar a un máximo de 300 mm en un ciclo único. Por lo tanto, los procesadores deben ser colocados cerca uno de otro para minimizar los retrasos de comunicación. Si las frecuencias de un reloj continúan incrementándose, la rapidez de la luz finalmente se convertirá en un factor límite para el diseño interno de chips individuales.
VELOCIDAD CONSTANTE PARA TODOS LOS MARCOS DE REFERENCIA
Es importante observar que la velocidad de la luz no es un límite de velocidad en el sentido convencional. Un observador que persigue un rayo de luz lo mediría al moverse paralelamente él mismo viajando a la misma velocidad como si fuese un observador estacionario. Esto conllevaría a consecuencias inusuales para la velocidad.
La mayoría de los individuos están acostumbrados a la regla de la adición de velocidades: si dos coches se acercan desde direcciones opuestas, cada uno viajando a una velocidad de 50 km/h, se esperaría (con un alto grado de precisión) que cada coche percibiría al otro en una velocidad combinada de 50 + 50=100 km/h.
Sin embargo, a velocidades cercanas a la de la luz, en resultados experimentales se hace claro que esta regla no se puede aplicar. Dos naves que se aproximen una a otra, cada una viajando al 90% de la velocidad de la luz relativas a un tercer observador entre ellas, no se percibirán mutuamente a un 90% + 90%=180% de la velocidad de la luz. En su lugar, cada una percibirá a la otra aproximándose a menos de un 99,5% de la velocidad de la luz. Este resultado se da por la fórmula de adición de la velocidad de Einstein:

donde v y w son las velocidades de las naves observadas por un tercer observador, y u es la velocidad de cualquiera de las dos naves observada por la otra.
Contrariamente a la intuición natural, sin importar la velocidad a la que un observador se mueva relativamente hacia otro observador, ambos medirán la velocidad de un rayo de luz que se avecina con el mismo valor constante, la velocidad de la luz.
La ecuación anterior fue derivada por Einstein de su teoría de relatividad especial, la cual toma el principio de relatividad como premisa principal. Este principio (originalmente propuesto por Galileo Galilei) requiere que actúen leyes físicas de la misma manera en todos los marcos de referencia.
Ya que las ecuaciones de Maxwell otorgan directamente una velocidad de la luz, debería ser lo mismo para cada observador; una consecuencia que sonaba obviamente equivocada para los físicos del siglo XIX, quienes asumían que la velocidad de la luz dada por la teoría de Maxwell es válida en relación al "éter lumínico".
Pero el experimento de Michelson y Morley, puede que el más famoso y útil experimento en la historia de la física, no pudo encontrar este éter, sugiriendo en su lugar que la velocidad de la luz es una constante en todos los marcos de referencia.
Aunque no se sabe si Einstein conocía los resultados de los experimentos de Michelson y Morley, él dio por hecho que la velocidad de la luz era constante, lo entendió como una reafirmación del principio de relatividad de Galileo, y dedujo las consecuencias, ahora conocidas como la teoría de la relatividad especial, que incluyen la anterior fórmula auto-intuitiva.
EXPERIMENTOS PARA RETARDAR LA LUZ
Fenómenos refractivos tales como el arco iris tienden a retardar la velocidad de la luz en un medio (como el agua, por ejemplo). En cierto sentido, cualquier luz que viaja a través de un medio diferente del vacío viaja a una velocidad menor que c como resultado de la refracción. Sin embargo, ciertos materiales tienen un índice de refracción excepcionalmente alto: en particular, la densidad óptica del condensado de Bose-Einstein puede ser muy alta.
En 1999, un equipo de científicos encabezados por Lene Hau pudo disminuir la velocidad de un rayo de luz a cerca de 17 m/s, y en 2001 pudieron detener momentáneamente un rayo de luz.
En 2003, Mijaíl Lukin, junto con científicos de la Universidad Harvard y el Instituto de Física Lébedev (de Moscú), tuvieron éxito en detener completamente la luz al dirigirla a una masa de gas rubidio caliente, cuyos átomos, en palabras de Lukin, se comportaron como «pequeños espejos» debido a los patrones de interferencia en dos rayos de control.
INTERFERENCIA DE LA LUZ
La interferencia es cualquier proceso que altera, modifica o destruye una onda durante su trayecto en el medio en que se propaga. La palabra destrucción, en este caso, debe entenderse en el sentido de que las ondas cambian de forma al unirse con otras; esto es, después de la interferencia normalmente vuelven a ser las mismas ondas con la misma frecuencia.
SUPERPOSICIÓN DE ONDAS
En la mecánica ondulatoria la interferencia es el resultado de la superposición de dos o más ondas, resultando en la creación de un nuevo patrón de ondas. Aunque la acepción más usual para interferencia se refiere a la superposición de dos o más ondas de frecuencia idéntica o similar. Matemáticamente, la onda resultante es la suma algebraica de las ondas incidentes, de tal forma que la función de onda en un punto es la suma de todas las funciones de onda en ese punto.
El principio de superposición de ondas establece que. Esto es consecuencia de que la Ecuación de onda es lineal, y por tanto si existen dos o más soluciones, cualquier combinación lineal de ellas será también solución.
SUPERPOSICIÓN DE ONDAS DE LA MISMA FRECUENCIA
En la superposición de ondas con la misma frecuencia el resultado depende de la diferencia de fase δ. Si sumamos dos ondas y1 = Asin(kx − ωt) y y2 = Asin(kx − ωt + δ), la onda resultante tendrá la misma frecuencia y amplitud 2A. Este tipo de interferencias da lugar a patrones de interferencia, ya que dependiendo de la fase, la interferencia será destructiva (las ondas se encuentran desfasadas 180 grados o π radianes) o constructiva (desfase de 0 grados/radianes).
La superposición de ondas de frecuencias ƒ1 y ƒ2 muy cercanas entre sí produce un fenómeno particular denominado pulsación (o batido).
En esos casos nuestro sistema auditivo no es capaz de percibir separadamente las dos frecuencias presentes, sino que se percibe una frecuencia única promedio (ƒ1 + ƒ2) / 2, pero que cambia en amplitud a una frecuencia de ƒ2 - ƒ1 .
Es decir, si superponemos dos ondas senoidales de 300 Hz y 304 Hz, nuestro sistema auditivo percibirá un único sonido cuya altura corresponde a una onda de 302 Hz y cuya amplitud varía con una frecuencia de 4 Hz (es decir, cuatro veces por segundo).
Las pulsaciones se perciben para diferencias en las frecuencias de hasta aproximadamente 15-20 Hz.
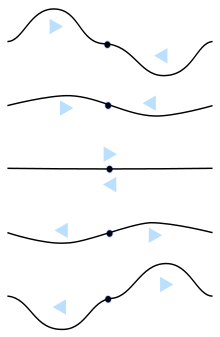
Sucesión (de arriba hacia abajo) de interferencia constructiva de ondas. El punto representa el antinodo y las flechas representan la dirección de las ondas.
PULSACIONES O BATIDOS
Si se da el caso de que la frecuencia de ambas ondas no es igual (f1,f2), pero si son valores muy cercanos entre sí, la onda resultante es una onda modulada en amplitud por la llamada "frecuencia de batido" cuyo valor corresponde a fbatido = Δf = | f1 − f2 | , la frecuencia de esta onda modulada corresponde a la media de las frecuencias que interfieren.
Este fenómeno se usa por ejemplo, para afinar instrumentos (por ejemplo, un piano y un diapasón), ya que cuando las pulsaciones desaparecen, esto quiere decir que las frecuencias de ambos instrumentos son iguales (o casi iguales a un nivel que el batido no es detectable).
Sucesión (de arriba hacia abajo) de una Interferencia destructiva. Las flechas representan la dirección de las ondas, mientras los puntos representan el nodo que produce la interferencia.
POLARIZACION DE LA LUZ
La polarización de la luz es uno de los fenómenos que contribuyo a establecer la teoría ondulatoria.
En una onda no polarizada la vibración oscila en todas las direcciones perpendiculares a la dirección de propagación. Partiendo de ese estado, la onda se polariza si por algún motivo (por ejemplo, después de atravesar un cristal) pasa a oscilar sólo en un determinado plano, al que se denomina plano de polarización. | ||

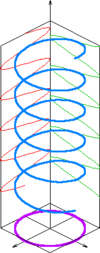
Fresnel fue uno de los primeros físicos que estudió en detalle fenómenos que manifiesta la luz polarizada. Comprobó que dos rayos polarizados ubicados en un mismo plano se interfieren, pero en cambio no lo hacen, si están polarizados entre sí, cuando se encuentran perpendicularmente. Esto le invitó a pensar que en un rayo polarizado debe ocurrir algo en la dirección perpendicular a la de propagación. Supuso que ese algo tiene que ser la propia vibración luminosa y en su modelo ondulatorio consideró a la luz una onda transversal. El propósito del experimento es estudiar el comportamiento de la luz después de atravesar dos láminas de plástico polarizadoras, observando y midiendo las variaciones que deberían producirse en la intensidad luminosa al cambiar la orientación relativa de dos láminas. veamos algunos casos donde se presente la polarizacion: Los tipos de polarizacion son: la forma trazada sobre un plano fijo por un vector de campo electrico de un vector de campo electrico de una onda plana que pasa sobre el es una CURVA DE LISSAJOUS y puede ser utilizada para describir el tipo de polarizacion de la onda. las siguientes figuras muestran algunos ejemplos de polarizacion: FIGURA 1  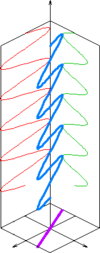 |
en la figura 1 de representa la polarización lineal y la oscilacion del plano perpendicularmente a la direccion de propagacion se produce a lo largo de una linea recta. se puede representarse cada oscilacion descomponiendola en dos ejes que son X e Y.
esta se produce cuando ambas componentes estan en fase ( con un angulo de DESFASE, cuando ambas componentes alcanzan sus maximos y minimos simultaneamente ) o en CONTRAFASE ( alcanza angulo de desfase de unos 180°, cuando cada uno de los componentes alcanza sus maximos a la vez que la otra alcanza sus minimos).
La relacion entre las amplitudes de ambos componentes determina la direccion de la oscilacion, que es la direccion de la polarizacion lineal.
En cualquier punto del espacio, el vector del campo eléctrico oscila arriba y abajo a lo largo de una línea vertical, y se dice que la onda está linealmente polarizada. La luz linealmente polarizada representa un tipo simple de polarización. La luz solar y la radiación emitida por la Tierra no están polarizadas. La luz natural contiene un número enorme de ondas, orientadas aleatoriamente. La luz emitida es una mezcla de ondas que están linealmente polarizadas en todas las direcciones transversales posibles.
FIGURA 2


En la figura 2 se represnta la polarizacion circular.
Los dos componentes ortogonales tiene exacatamente la misma amplitud y estan desfasadas exactamente 90°. en este caso , un componente se anula cuando el otro componente alcanza su amplitud maxima o minima.
Existen dos relaciones posibles que satisfacen esta exigencia, de forma que el componente X puede estar 90° adelantado o retrasado respecto al componente Y. el sentido ( HORARIO O ANTI HORARIO ) en el que gira el campo electrico depende de cual de estas dos relaciones sede.FIGURA 3

En la figura 3 se representa la polarizacion ELIPTICA . esta tipo de polarizacion corresponde a cualquier otro caso diferente a los anteriores, es decir, los dos componentes tienen distancias amplitudes y el angulo de desfase entre ellas es diferente a 0° y a 180°
( NO ESTAN NI EN FASE NI EN CONTRAFASE ).
LA FOTOMETRIA
La fotometria es la ciencia que es la encargada de la medida de la luz, como el brillo percibido por el ojo humano.
Estudia la capacidad que tiene la radiacion electromagnética de estimular el sistema visual. No debe confundirse con la RADIOMETRIA, encargada de la medida de la luz en terminos de potencia absoluta.
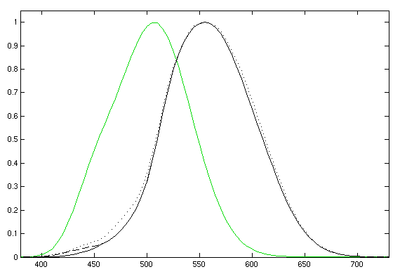
Función de luminosidad fotópica (negro) y función de luminosidad escotópica (verde). La fotópica incluye la función CIE 1931 estándar (sólida), la modificación de Judd-Vos de 1978 (línea de guiones), y los datos de Sharpe, Stockman, Jagla & Jägle de 2005 (línea de puntos). Muestra la sensibilidad relativa del ojo a las diferentes longitudes de onda. El eje horizontal es la longitud de onda en nanómetros.
El ojo humano no tiene la misma sensibilidad para todas las logitudes de onda que forman el espectro visible.
El ojo humano no tiene la misma sensibilidad para todas las logitudes de onda que forman el espectro visible.
La fotometria introduce este hecho ponderando las diferentes magnitudes radiometricas medidas para cada longitud de onda por un factor que representa la sensibilidad del ojo modelo, que suele denotar como
 ,
, o
o ( este modelo u observador estandar es muy similar a los de la calorimetria ). Esta funcion es diferente dependiendo de que el ojo se encuentre adaptado a condiciones buena de iluinacion ( vision fotopica ) o de mala ( visión escotopica ). Asi, en condiciones fotocopicas, la curva alcanza su pico para 555 nm, mientras que en condiciones escotopicas lo hace para 507 nm.
( este modelo u observador estandar es muy similar a los de la calorimetria ). Esta funcion es diferente dependiendo de que el ojo se encuentre adaptado a condiciones buena de iluinacion ( vision fotopica ) o de mala ( visión escotopica ). Asi, en condiciones fotocopicas, la curva alcanza su pico para 555 nm, mientras que en condiciones escotopicas lo hace para 507 nm.RELACIÓN CON LA RADIOMETRIA
Por ejemplo la magnitud radiometrica de la ENERGIA RADIANTE,  , que describe la enegria total medida por un detector "fisico" ante la presencia de radiacion elcetromagnetica. interesa obtener una medida de la energia que seria percibida por un ojo humano: CANTIDAD DE LUZ,
, que describe la enegria total medida por un detector "fisico" ante la presencia de radiacion elcetromagnetica. interesa obtener una medida de la energia que seria percibida por un ojo humano: CANTIDAD DE LUZ,  .
.
 , que describe la enegria total medida por un detector "fisico" ante la presencia de radiacion elcetromagnetica. interesa obtener una medida de la energia que seria percibida por un ojo humano: CANTIDAD DE LUZ,
, que describe la enegria total medida por un detector "fisico" ante la presencia de radiacion elcetromagnetica. interesa obtener una medida de la energia que seria percibida por un ojo humano: CANTIDAD DE LUZ,  .
.para ello, habria que conocer la energia radiante correspondiente a cada longitud de onda, multiplicar por los valores correspondientes de la funcion de luminosidad e integrar a todas las longitudes de onda:

La energia radiante espectral,  , se mide en el SI en unidades de J/m.
, se mide en el SI en unidades de J/m.
 , se mide en el SI en unidades de J/m.
, se mide en el SI en unidades de J/m.En cambio,  se mide en lm·s la constante K toma el valor de 638 lm/W en condiciones fotopicas y de 1700 lm/W para condiciones escotopicas.
se mide en lm·s la constante K toma el valor de 638 lm/W en condiciones fotopicas y de 1700 lm/W para condiciones escotopicas.
 se mide en lm·s la constante K toma el valor de 638 lm/W en condiciones fotopicas y de 1700 lm/W para condiciones escotopicas.
se mide en lm·s la constante K toma el valor de 638 lm/W en condiciones fotopicas y de 1700 lm/W para condiciones escotopicas.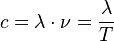



No hay comentarios:
Publicar un comentario