RAYO DE LUZ

las lineas rectilíneas representan los rayos luminosos, que en la ilustración se reflejan y refractan en la fina película de una pompa de jabón.
La utilizacion de este modelo, ampliamente divulgado en optica geometrica, simplificado los calculos debido al principio de propagacion en linea recta de la luz en medios homogeneos e isotropos, como lo son el aire o el agua. en óptica física, el rayo es la trayectoria que teóricamente recorre la energía luminosa. En la teoría corpuscular de la luz, el rayo luminoso representa la trayectoria de los fotones, perdiendo todo significado cuando los efectos de la mecánica cuantica comienzan a apreciarse.
Trayectoria que teóricamente recorre la energía luminosa. En la teoría corpuscular de la luz, el rayo luminoso representa la trayectoria de los fotones, perdiendo todo significado cuando los efectos de la mecánica cuántica comienzan a apreciarse.
Cabe aclarar que el concepto de rayo pierde su utilidad cuando los fenómenos de difracción empiezan a tomar un papel relevante; por ejemplo, cuando un haz de luz pasa a través de una abertura comparable a la longitud de onda del propio haz.

rayos luminoso que se encuentran con una superficie rugosa, dispersándose en todas direcciones.
REFLEXIÓN DE LA LUZ
La reflexión es el cambio de dirección de un rayo o una onda que ocurre en la superficie de separación entre dos medios, de tal forma que regresa al medio inicial. ejemplos comunes son la reflexión de la luz, el sonido y las ondas en el agua.
REFLEXIÓN DE LA LUZ Y SUS LEYES
Es el cambio de dirección, en el mismo medio, que experimenta un rayo luminoso al incidir oblicuamente sobre una superficie. para este caso las y es de la reflexión son las siguientes:
PRIMERA LEY:
El rayo incidente, el rayo reflejado y la normal, se encuentran en un mismo plano.
SEGUNDA LEY:
El angulo de incidencia es igual al angulo de reflexión.

i: angulo de incidencia.
r: angulo de reflexión.
RETROREFLECTOR
La retrorreflexion en la capacidad que tiene algunas superficies que por su estructura pueden reflejar la luz de vuelta hacia la fuente, sin que me importe el angulo de incidencia original.
Este comportamiento se puede observar en un espejo, pero únicamente cuando este se encuentra perpendicularmente a la fuente, es decir, cuando el angulo de incidencia es igual a 90°. se puede construir un RETROREFLECTOR simple colocando tres espejos ordinarios de forma que todos sean perpendiculares entre si (un reflector esquinero). la imagen que se produce es igual a la imagen producida por un espejo pero invertida. tal como se observa en la figura, la combinación de las diferentes superficies hace que el haz de luz sea reflejado de vuelta a la fuente.
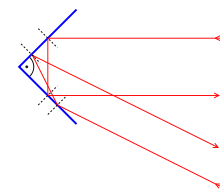
principio de funcionamiento de un reflector de esquina.
Si a una superficie se le aplica una pequeña capa de esferas reflectivas es posible obtener una superficie con una capacidad limitada de retrorreflexion. El mismo efecto se puede obtener si se dota a la superficies con una estructura similar a pequeñas pirámides (reflexión esquinera). En ambos casos, la estructura interna de la superficie refleja la luz que incide sobre ella y la envía directamente hacia la fuente. Este tipo de superficies se utilizan para crear las señales de tránsito y las placas de los automóviles; en este caso particular no se desea una retrorreflexion perfecta, pues se quiere que la luz retorne tanto hacia las luces del vehículo que emite el haz de luz como a los ojos de la persona que lo va conduciendo.
IMÁGENES DE REFLEXIÓN
La reflexión de la luz se representa por medio de dos rayos: el que llega a una superficie, rayo incidente, y el que sale "rebotado" después de reflejarse, rayo reflejado.
si se traza una recta perpendicular a la superficie ( que se denomina normal ), el rayo incidente forma un angulo con dicha recta, que se llama angulo de incidencia.

El ángulo de refraccion r se corresponde con el ángulo de incidencia i y los índices de refracción del aire (n1) y la superficie (n2). Así, si el índice de la superficie es 1,5 y el del aire 1, si el ángulo de incidencia fuera de 45º, el ángulo de refracción sería 28º.
Además, cabe la posibilidad de que la materia absorba la luz, o la disperse. La luz dispersada o reflejada puede terminar por salir por el frente, la parte de atrás o un costado del objeto iluminado.

En esta imagen donde aparecen los pelícanos se puede apreciar que la silueta de ellos se refleja en el agua, seria una reflexión especular ya que pareciese que se estuviera reflejando en un espejo.
En esta imagen de un paisaje natural podemos observar que la reflexión es especular ya que la imagen se puede ver como si se estuviera visualizando en un espejo.
En esta imagen donde podemos observar que la imagen es reflexión difusa ya que la no se conserva la imagen pero la energía se conserva.

En esta imagen de la cascada podemos observa que la imagen es interferida por el agua que cae por eso la imagen es de reflexión difusa ya que no se puede visualizar bien la imagen pero la energía del objeto se conserva.
ESTE VÍDEO SE TRATA SOBRE LA REFLEXIÓN DE LA LUZ ESPERAMOS QUE LES GUSTE Y ACLAREN SUS DUDAS SI TODAVÍA TIENEN ALGUNAS ESPERAMOS QUE LES GUSTE....
ESPEJOS ESFÉRICOS
Los espejos esféricos tienen la forma de la superficie que resulta cuando una esfera es cortada por un plano. Si la superficie reflectora está situada en la cara interior de la esfera se dice que el espejo es cóncavo. Si está situada en la cara exterior se denomina convexo. Las características ópticas fundamentales de todo espejo esférico son las siguientes:
su formula es n=360/<a-1. Donde n=numero de imágenes, 360=< perigonal, <a=angulo de abertura, -1=el objeto reflejado.
Centro de curvatura C: Es el centro de la superficie esférica que constituye el espejo.
Radio de curvatura R: Es el radio de dicha superficie.
Vértice V: Coincide con el centro del espejo.
Eje principal: Es la recta que une el centro de curvatura C con el vértice V.
Foco: Es un punto del eje por el que pasan o donde convergen todos los rayos reflejados que inciden paralelamente al eje. En los espejos esféricos se encuentra en el punto medio entre el centro de curvatura y el vértice.

Se denomina rayos paraxiales a los rayos más próximos al eje óptico. En el estudio de los espejos esféricos, estudiaremos únicamente los rayos próximos al eje óptico, debido a que todos los rayos paralelos que convergen en su superficie los hacen converger en un punto que llamaremos Foco.
Es lo que se conoce como aproximación paraxial.
Llamamos espejo esférico a una porción de superficie esférica pulimentada. Son cuando su superficie interior es reflectante y convexos cuando lo es la exterior.

Los rayos no paraxiales se reflejan en un espejo esférico cóncavo, se intersecan en el eje óptico en diferentes puntos y resulta una imagen borrosa. Esto se llama aberración esférica.

consideramos un espejo cóncavo en el que se reflejan los rayos paraxiales que provienen del objeto O para converger en l dando se forma la imagen. C es el centro de la curvatura, P es el punto de incidencia con el espejo. por la ley de reflexión el rayo incidente con le espejo. por la ley de reflexión el rayo incidente y el reflejado tiene el mismo angulo.
Llamamos S0 a la distancia desde 0 al vértice V, Si a la distancia entre el punto imagen, I y el vértice. La distancia CV es el radio de curvatura r. Según la figura y considerando que los ángulos son muy pequeños, podemos hacer las siguientes aproximaciones:
tg α ≈ α ≈ 1/So
tg β ≈ β ≈ 1/r
tg θ ≈ θ = 1/Si
En el triángulo OPI tenemos que α + 2.i + (180º - θ) = 180º; de donde α + 2.i = θ.
De la misma forma, en el triángulo CPI, tenemos que:
β + i + (180º - θ) = 180º; de donde i = θ - β.
Sustituyendo en la primera α + 2.(θ - β) = θ;
α + θ = β.
Ecuación de los espejos: 1/So + 1/Si = 2/r
Si O está muy distante de forma que 1/So ≈ 0, entonces Si = r/2 .
En este caso, se puede considerar que los rayos son prácticamente paralelos, puesto que vienen de un punto muy alejado, y por tanto, los reflejados convergen en un punto que llamábamos foco. En este caso el foco coincide con la imagen y Si es la distancia focal f = r/2
Entonces se puede escribir:
1/So + 1/Si = 1/f


Es valido tanto para espejos cóncavos como convexos. Solo depende del criterio de signos que se utilice.
Criterio de signos
S0 es + si el objeto está enfrente del espejo (objeto real)
S0 es - si el objeto está detrás del espejo (objeto virtual)
Si es + si la imagen está enfrente del espejo (imagen real)
Si es - si la imagen está detrás del espejo (imagen virtual)
f y r son + si el centro de curvatura está enfrente del espejo (cóncavo) y - si está detrás (convexo).
¿Puede emplearse la ecuación de los espejos esféricos para un espejo plano?
Se puede suponer, al igual que suponemos que un fuente de onda esférico es plano cuando está a gran distancia del foco emisor, que un espejo plano es como un esférico de radio ∞. Por tanto:
1/So + 1/Si = 2/∞
So = Si
Esto es efectivamente una descripción de lo que sucede en un espejo plano: La imagen es virtual, es decir, negativa, pero las distancias son iguales.
No hay comentarios:
Publicar un comentario